プロアフィリエイターに見られたら怒られそうなふざけたタイトルのつけ方ですが、今回は掲題の件についての独り言。
途中ちょこちょこスロットの話が出てくるので、スロッター出身の方じゃないとピンと来ない部分があるかも。
というかそもそも全体的に需要がありそうな内容でない事はわかっているんだけど、前回の記事のまま終わるのはちょっといかがなものか?という感じもするのでその続きです。
ちょっと興味あるよ、って方は「ふ~ん」くらいの感覚で読んでみてください。
推測統計学の話
前回の記事でも書いた通りだが、シストレにおける期待値とはなんぞや?という部分がずっと引っ掛かっていた。
このモヤモヤが原因でシストレに身が入らないのはよくないという事で、期待値の基とも言える統計学について少しだけ勉強してみた。
統計学を大きく分類すると「記述統計学」と「推測統計学」に分かれるのだが、期待値を考える上で大事なのは後者の「推測統計学」の方。
いや、そも推測統計学ってなんぞや?って話になると思うのだが、wiki先生曰く「無作為抽出された部分集団(抽出集団、標本集団)から抽出元全体(母集団)の特徴、性質を推定する統計学」の事を指すらしい。
当然文字だけ見てもよくわからない。
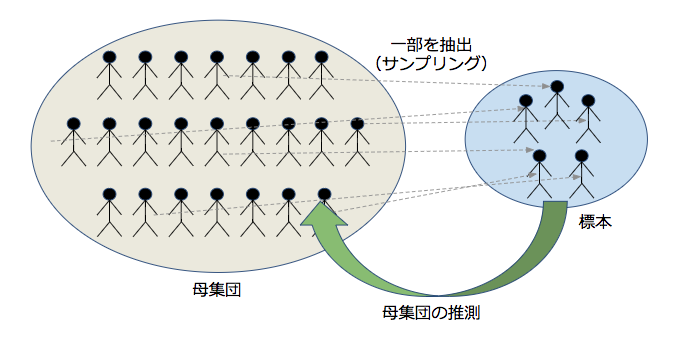
上にあるのは拾い物の図であるが、要はこういう事である。
50人のクラスを母集団と仮定すると、無作為に抽出された5人の生徒が標本。
5人の生徒(標本)からその身長、体重について調べ、クラス全体(母集団)の平均身長、体重といった性質を推測するのが推測統計学。
この推測ってところがミソだと思う。
サイコロの話
もう一つよくあるサイコロを例に出した話。
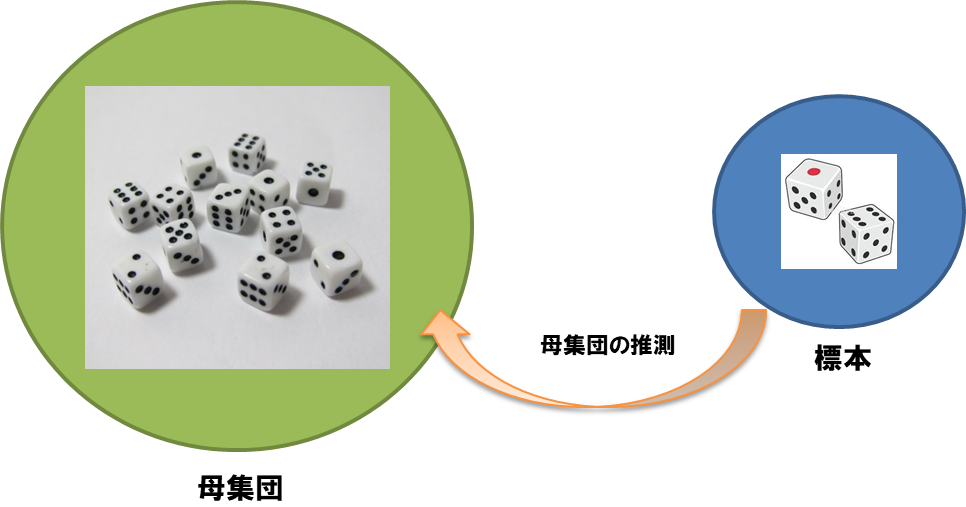
サイコロの出目を母集団、実際に振って出た出目の記録を標本とみなし、標本から母集団の性質を調べる。
1,6,6,2,5,1,3,1,4,6,3・・・
ふむふむ。サイコロを一回振った時の平均値(期待値)って3.5っぽいな!!!
これは例であり、もちろん実際にはこんな事する必要がない。
なぜならわれわれは下に書いたようなサイコロの性質を知っているからだ。
①6面で出来ている。
②その6面には1~6の数値が振られている。
③均等に6面が出る構造体である。
④①~③の事からサイコロを一回振った時の出目期待値は3.5である。
ここで少しスロットの話をしてみる。
俺が普段から行っているスロットの期待値稼働は、上の例でいうと「サイコロを振る→3以上が出たら勝ち、2以下なら負け」という勝負を繰り返しているだけに過ぎない。
簡単なもんだ。だってスロットの場合その解析情報がネットで調べたら一瞬で出てくる。
つまりは①~④の情報を事前に与えられているわけだからね。
これに対し株はどうか?
出目しか情報がない。
トレード記録はもちろんの事、テクニカル指標や本に載っている様々な売買方法だって過去のトレードから裏付けされたものと考えると、これらは広義で出目と言える。
つまり株の世界では1,6,6,2,5・・・といった出目から①~④を推測する必要がある。まあ正確には④だけでいい気もするが。
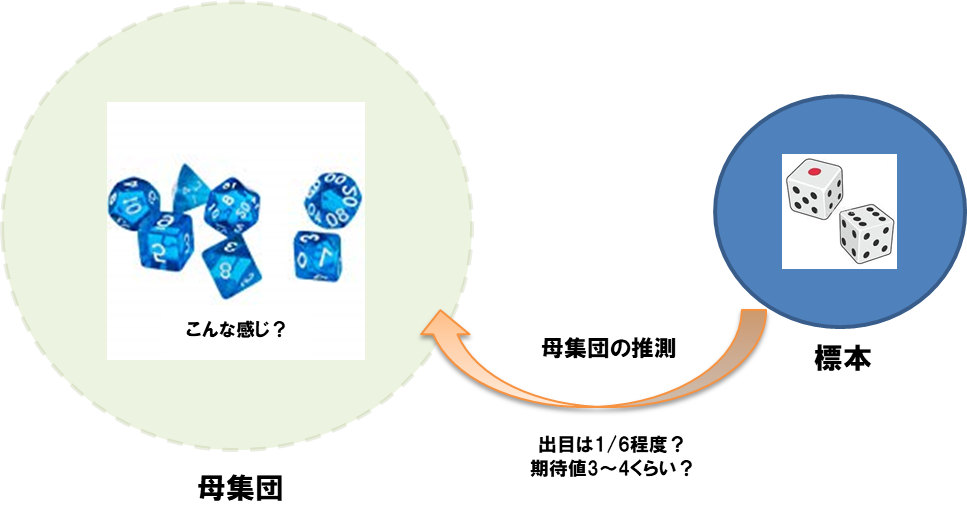
そしてその上で「3以上が出たら勝ち、2以下なら負けという勝負を継続すれば勝てるんじゃね?」という推論に行き着く。
そしてそして行き着いたその推論を根気よく続けて初めて勝利への道が見えてくる。
・・・どう考えたって難易度が段違いだと思うんだ。
そりゃスロットの世界でも店選びとかである程度差は出てくる。
でもそれって3以上が出たら勝ち、2以下なら負けという条件だと勝負してくれる人がいないから、3回振って10以上が出たら勝ち、9以下なら負けという勝負に作戦を変えるとかそういうレベルの話だから。
出目期待値3.5という絶対的な情報を持っていて負けようなんてないんだよ本来。
以前、スロットで食っていきたいから弟子入りさせてくれと頼みにきた友人がいた。その友人はあまりに見込みがなく、スロットを教える事を数日で辞めた。
そしてしばらくした後、今度は株で食っていきたいから株を教えてくれ、と頼みに来た。
当然俺はこう言って跳ねのけた。
「スロットで勝てない奴が株で勝てるわけないから。」
その時はこの言葉の意味を深く考えなかったが、今になると上記の理由から難易度が段違い、という事を理論的に説明する事が出来る気がする。
株で生き残る確率は10%とよく耳にするが、一方でスロットで勝つ人も10%と言われている。
本当かこれ???にわかに信じがたいぞ。
まあ株はほぼ100%金銭の増減が主たる目的となっているのに対し、スロットはそのゲーム性を楽しむという目的の層も一定数いるので一概な比較は出来ないが・・・。

気付けばこの記事も結構な文字数になってきている。というかなんか疲れてきた。
当初タイトルの件を一記事にまとめようと思っていたのだが、このペースじゃ到底無理だ。
・・・という事で予定を変更し、全二部作、ないし三部作とさせていただく。
GW中には完結させるぞ!(予定)
